每日算法打卡：递归实现排列型枚举

算法
844 words

原题链接

94. 递归实现排列型枚举

题目难度：简单

题目描述

把 $ 1 \sim n $ 这 $ n $ 个整数排成一行后随机打乱顺序，输出所有可能的次序。

输入格式

一个整数 $ n $。

输出格式

按照从小到大的顺序输出所有方案，每行 $ 1 $ 个。

首先，同一行相邻两个数用一个空格隔开。

其次，对于两个不同的行，对应下标的数一一比较，字典序较小的排在前面。

数据范围

$ 1 \le n \le 9 $

输入样例：

1
3

输出样例：

1
2
3
4
5
6
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1

题目分析

这道题的意思很简单，就是生成从$ 1 \sim n $的全排列，第二个要求就是要按照字典序从小到大输出，字典序就是对于两个序列或者字符串，从头开始比较，只要相同就向后移动，不同的话就是谁小谁的字典序就小，如果都相同就是字典序相同，规定短的序列字典序较小

我们看到数据范围是到$ 9 $的，因此我们可以大致判断出这个题的时间复杂度限制在$O(n*n!)$即可

我们在枚举全排列时有两种方式

第一种是依次枚举每个数放到不同的位置，即固定选择一个数，按照不同位置分类

第二种是依次枚举每个位置放不同的数，即固定选择一个位置，按照不同的数分类

对于本质上的算法其实是一样的，对于具体理解其实是不太相同的

为了便于画图，我们采取第二种方式，画出递归搜素树

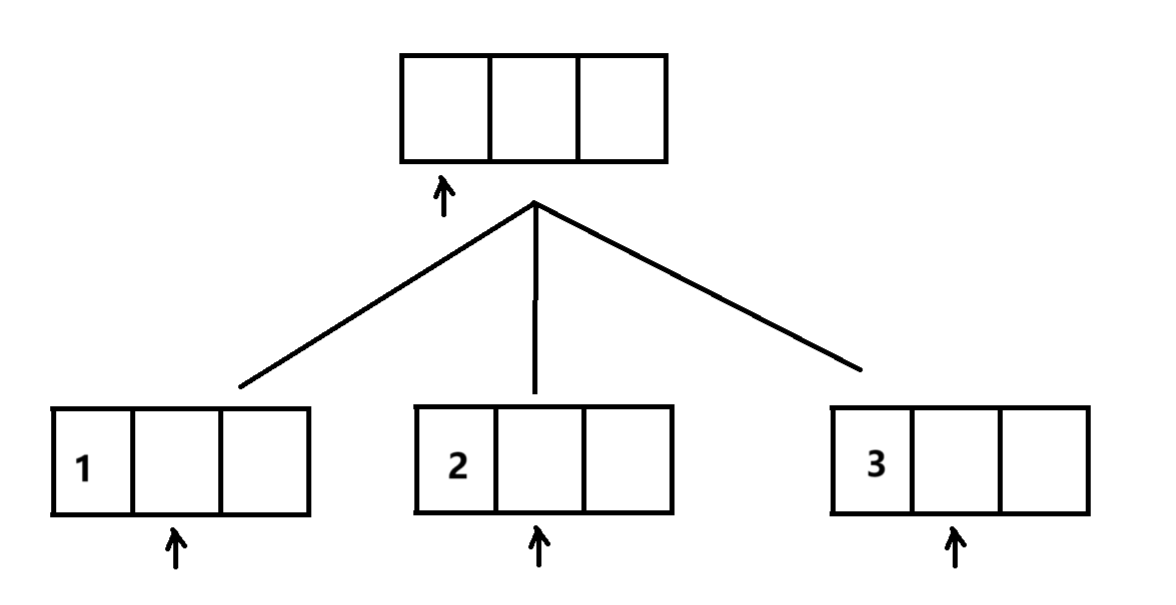
屏幕截图 2024-01-02 114116.png

我们就可以通过这样一个过程，依次枚举每个位置，将不同的数字放入其中，直到我们枚举到最后一个位置，将答案输出即可

我们也需要记录每个位置的状态，可以采用数组或者数位来记录，这里我们同样采用数组的方式，除此之外，我们需要记录哪些数字被用过，因此我们需要一个布尔数组来记录

示例代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
#include<iostream>
using namespace std;

const int N = 10; // 数据范围，为了方便理解，我们直接取从1到n，因此需要开十个空间

int n;
int state[N]; // 记录状态的数组，每个位置上填入已经选中的数字
bool used[N]; // 记录是否被使用过，未被使用则为false，使用过则为true

void dfs(int cur) // cur表示当前枚举到第cur位
{
    // 首先判断何时递归完成
    if (cur > n)// 这里表示我们已经把最后一个位置的数据枚举完成了
    {
        for (int i = 1; i <= n; i++) // 输出结果
            cout << state[i] << ' ';
        cout << '\n';
        return;
    }

    // 枚举每个数字，填入state数组
    for (int i = 1; i <= n; i++)
    {
        if (used[i] == false) // 如果未被使用
        {
            state[cur] = i; // 填入数字i
            used[i] = true; // 表示该数字被使用过了
            dfs(cur + 1); // 递归到下一个位置进行处理

            // 恢复未使用时的状态
            state[cur] = 0;
            used[i] = false;
        }
    }
}

int main()
{
    cin >> n;
    dfs(1); // 表示从第一个位置开始枚举
    return 0;
}
Comments