每日算法打卡：分巧克力

原题链接

1227. 分巧克力

题目难度：简单

题目来源：第八届蓝桥杯省赛C++ A/B组,第八届蓝桥杯省赛Java A/B/C组

题目描述

儿童节那天有 K 位小朋友到小明家做客。

小明拿出了珍藏的巧克力招待小朋友们。

小明一共有 N 块巧克力，其中第 i 块是 $H_i \times W_i$ 的方格组成的长方形。

为了公平起见，小明需要从这 N 块巧克力中切出 K 块巧克力分给小朋友们。

切出的巧克力需要满足：

1. 形状是正方形，边长是整数
2. 大小相同

例如一块 $6 \times 5$ 的巧克力可以切出 6 块 $2 \times 2$ 的巧克力或者 2 块 $3 \times 3$ 的巧克力。

当然小朋友们都希望得到的巧克力尽可能大，你能帮小明计算出最大的边长是多少么？

输入格式

第一行包含两个整数 N 和 K。

以下 NN 行每行包含两个整数 $H_i$ 和 $W_i$。

输入保证每位小朋友至少能获得一块 $1 \times 1$ 的巧克力。

输出格式

输出切出的正方形巧克力最大可能的边长。

数据范围

$1 \le N,K \le 10^5$,
$1 \le H_i,W_i \le 10^5$

输入样例：

2 10
6 5
5 6 

输出样例：

2 

题目分析

这道题就是将n个矩形，切出尽可能大的等长的k个正方形，求最大的可能正方形边长

我们可以发现一个规律，边长越大，切出来的正方形个数就越少，那我们其实是可以用公式表示出来每一个矩形能切多少块正方形的

假设正方形边长为x，最终切出来的正方形个数就是

$\lfloor \frac{W_i}{x} \rfloor \times \lfloor \frac{H_i}{x} \rfloor$

这样，我们就可以看出来，块数是和边长一定是一个递减的函数关系

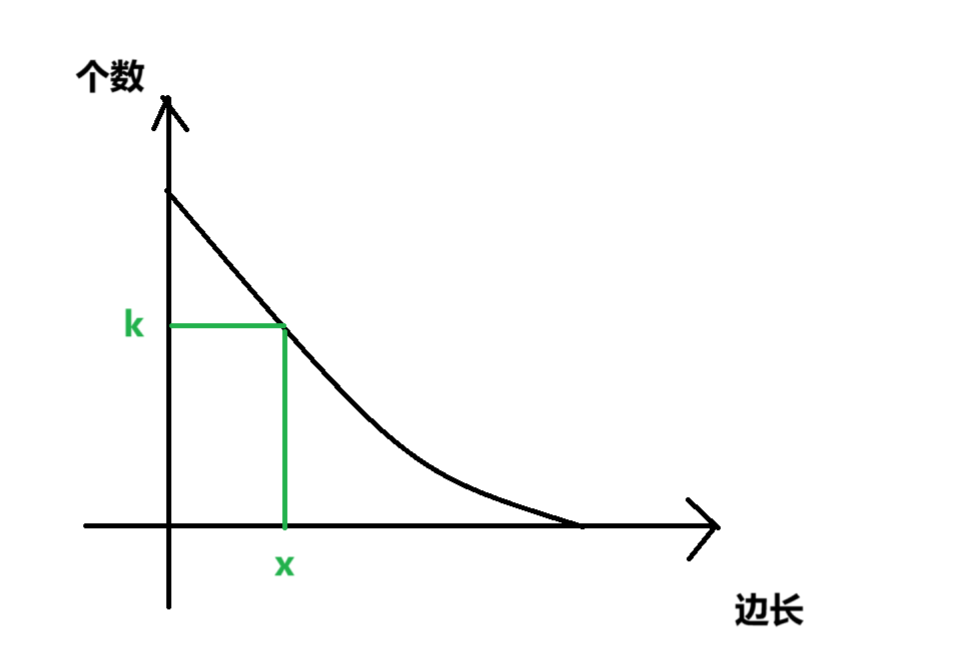
我们需要找到一个个数大于等于k的对应的x的最大值

实际上就只需要找到对应的这个点，我们就可以使用二分的做法

那么判断的条件就是满足块数大于等于k的x的最大值

我们分情况来判断，假如x从小到大递增

如果中间值$x_{mid}$大于等于k是成立的，说明说明，比中间值小的所有数字，都是满足条件的，因此我们就要让左边界更新为中心值

示例代码

#include<iostream>
using namespace std;

const int N = 1e5 + 10;

int n, k;
int h[N], w[N]; // 分别代表每一块的高度和宽度

bool check(int mid) // 判断块数是否大于k
{
    int res = 0; // 一共可以分成多少块
    for (int i = 0; i < n; i++)
    {
        res += (w[i] / mid) * (h[i] / mid); // 注意括号
        if (res >= k)
            return true;
    }
    return false;
}
int main()
{
    cin >> n >> k;
    for (int i = 0; i < n; i++)
        cin >> h[i] >> w[i];

    int l = 1, r = 1e5;
    while (l < r)
    {
        int mid = (l + r + 1) / 2;
        if (check(mid))
            l = mid;
        else
            r = mid - 1;
    }
    cout << r << '\n';
    return 0;
}