每日算法打卡：逆序对的数量

原题链接

788. 逆序对的数量

题目难度：简单

题目描述

给定一个长度为 n 的整数数列，请你计算数列中的逆序对的数量。

逆序对的定义如下：对于数列的第 i 个和第 j 个元素，如果满足 i < j 且 a[i] > a[j]，则其为一个逆序对；否则不是。

输入格式

第一行包含整数 n，表示数列的长度。

第二行包含 n 个整数，表示整个数列。

输出格式

输出一个整数，表示逆序对的个数。

数据范围

$1 \le n \le 100000$，
数列中的元素的取值范围 $[1,10^9]$。

输入样例：

6
2 3 4 5 6 1 

输出样例：

5 

题目分析

逆序对首先数对，他是一个线性代数中的概念，简单的理解就是，前面的数字比后面的数字大就是一个逆序对，需要注意的是，如果两个数字相同，则应该标记为不同的数字，只是数值相同

我们主要的思想还是采用分治，可以借用归并排序的思路，在归并排序的过程中计算出这个问题的答案

对于分治来说，如何不重不漏的将情况分出来是最重要的

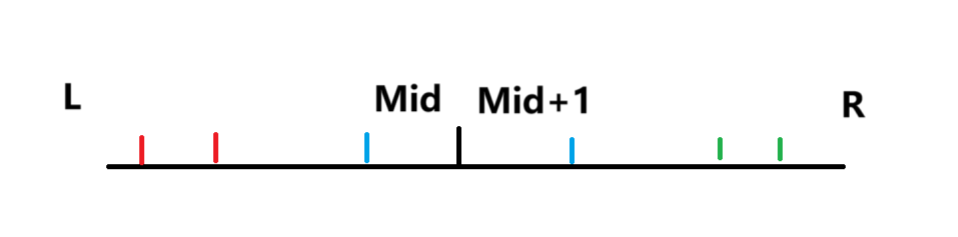
假设这是某一次分治的结果，分为[L,Mid]和[Mid+1,R]两个区间，红绿蓝表示可能出现的逆序对的位置

这一次分治的结果返回的是[L,R]的，所以结果应该是红色加蓝色加绿色

红色的结果是再对[L,Mid]进行归并排序的结果

绿色的结果是再对[Mid+1,R]进行归并排序的结果

那么难点就是对于蓝色的

我们假设左半边和右半边已经排号序了

此时画出图形就是这样的

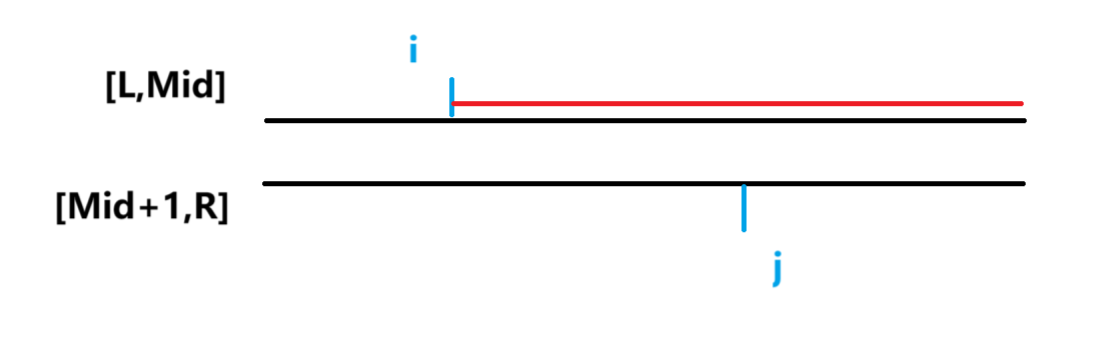
假设我们使用双指针，找到了一个a[j]<a[i]那么由于这两部分都是有序的，a[i]后面的所有数字都是严格大于a[j]的

通过这种方式就可以在归并的过程中计算出蓝色部分的个数了

示例代码

#include<iostream>
using namespace std;
using ll = long long;

const int N = 100010;

int n;
int a[N], tmp[N]; // tmp 存储中间结果

ll merge_sort(int l, int r)
{
    if (l >= r) return 0;
    int mid = l + r >> 1;
    ll res = merge_sort(l, mid) + merge_sort(mid + 1, r);

    int k = 0, i = l, j = mid + 1;
    while (i <= mid && j <= r)
    {
        if (a[i] <= a[j]) tmp[k++] = a[i++];
        else
        {
            tmp[k++] = a[j++];
            res += mid - i + 1;
        }
    }

    while (i <= mid) tmp[k++] = a[i++];
    while (j <= r) tmp[k++] = a[j++];

    for (i = l, j = 0; i <= r; i++, j++)
        a[i] = tmp[j];
    return res;

}

int main()
{
    cin >> n;
    for (int i = 0; i < n; i++) cin >> a[i];

    cout << merge_sort(0, n - 1) << '\n';
    return 0;
}