算法基础之树状数组

树状数组

树状数组能解决的最关键的问题就是能够$O(\log n)$内，给某个位置上的数，加上一个数，或者求前缀和

他和前缀和数组的区别就是，树状数组支持修改原数组的内容，而前缀和数组不支持，需要重新求前缀和数组

总结一下树状数组能做的操作就是单点修改和区间查询，对于他的其他的功能，例如区间修改，单点查询，区间修改，区间查询都是使用差分的思想转化成最基础的思想

这里我们需要利用图像来表示

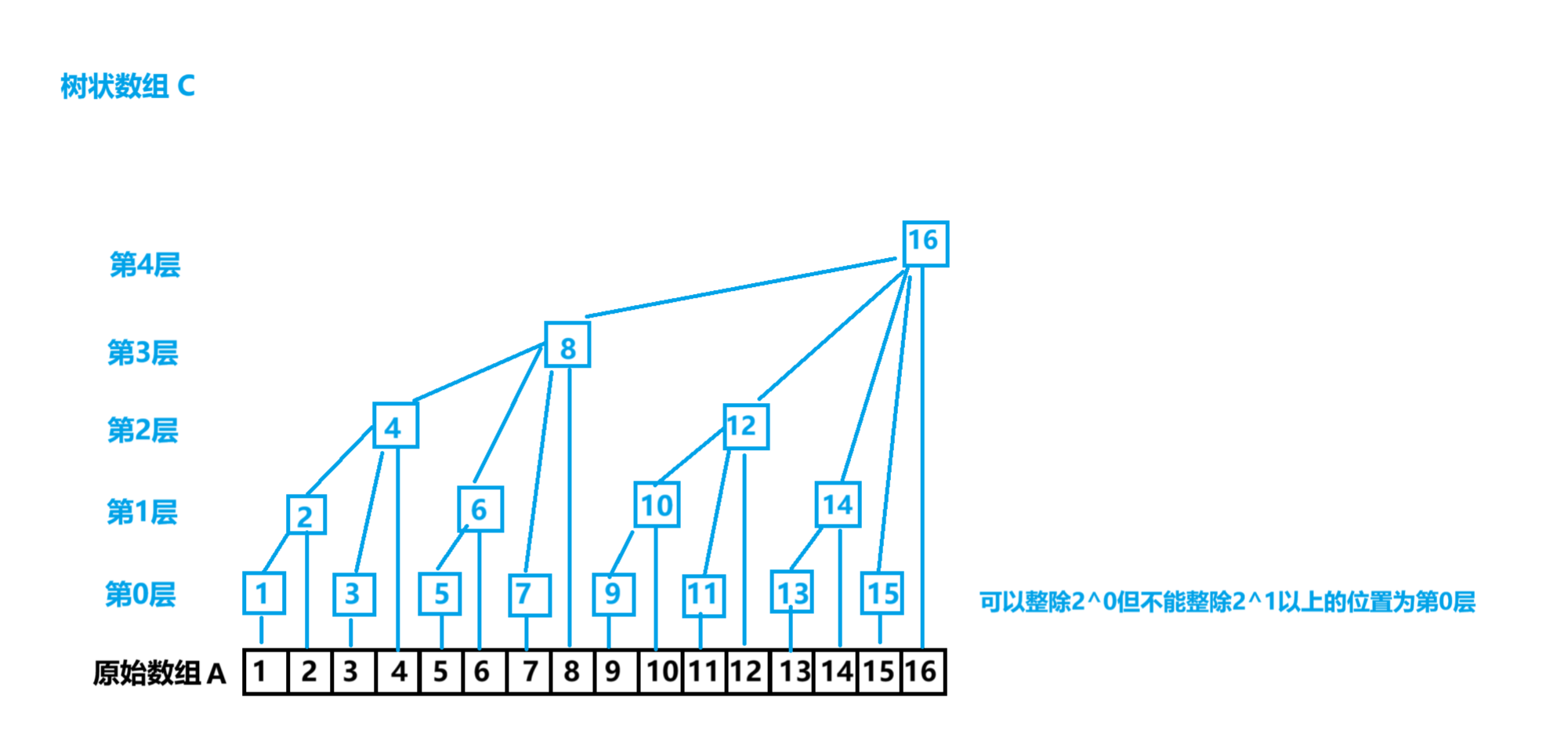
这里的树状数组虽然画出来是个树，但本质上还是一维数组

其中的任意一个数字其实表示的是一段数的和，例如$C[8]=A[1]+\dots+A[8]$

那么对于$C[x]$，我们如何确定x的层数呢，其实是可以利用x的二进制表示，其中末尾有几个0，就是第几层的数字，假设他最后有k个0，那么$C[x]=\sum_{x-2^k+1}^xA[x]$，C++中有一个lowbit(x)函数，可以返回$2^k$,因此这个表达式也可以写成$C[x]=\sum_{x-lowbit(x)+1}^xA[x]$，补充这里这里的lowbit(x)函数的原理就是位运算$x&-x$

有了这部分的原理之后，我们就可以有两个操作

首先就是求前缀和，例如我们想求前x项的和，结果就是$C[x]+C[x-lowbit(x)]+\dots$

写成代码就可以是

int res = 0;
for(i=x;i>0;i-=lowbit(x))
{
    res += c[i];
}
return res;

那比较难理解的就是更新的过程，假设我们要给A[x]+v，严格证明过于复杂，我们这里只给出出结论和代码

由于我们更改了原数组中的一个数值，那么他对应的所有父节点的数值都需要更改，那么x的父节点其实就是x+lowbit(x)，给出代码如下

for(i=x;i<=n;i+=lowbit(x))
{
    c[x] += v;
}