C++手撕AVL树

C++
1.4k words

AVL树

之前我们讲了二叉搜索树的相关内容，但是也了解到二叉搜索树有其自身的缺陷，就是当插入的元素有序或者接近有序，退化成单支树的时候，他的时间复杂度就会退化成O(N)，因此我们需要对他进行优化，有两种，一种是AVL树，也就是平衡二叉树，另一种是红黑树，这里我们先介绍AVL树

概念

在发现这个问题之后，两个俄罗斯数学家发明了解决这个问题的一种办法

当向二叉搜索树中插入节点之后，检查每个节点的左右子树高度只差绝对值不超过一，否则需要进行调整

这样就能降低树的高度，从而减少平均的搜索长度

一棵AVL树是空树或者有如下性质

  • 左右子树都是AVL树
  • 左右子树高度差（平衡因子）的绝对值不超过1

例如

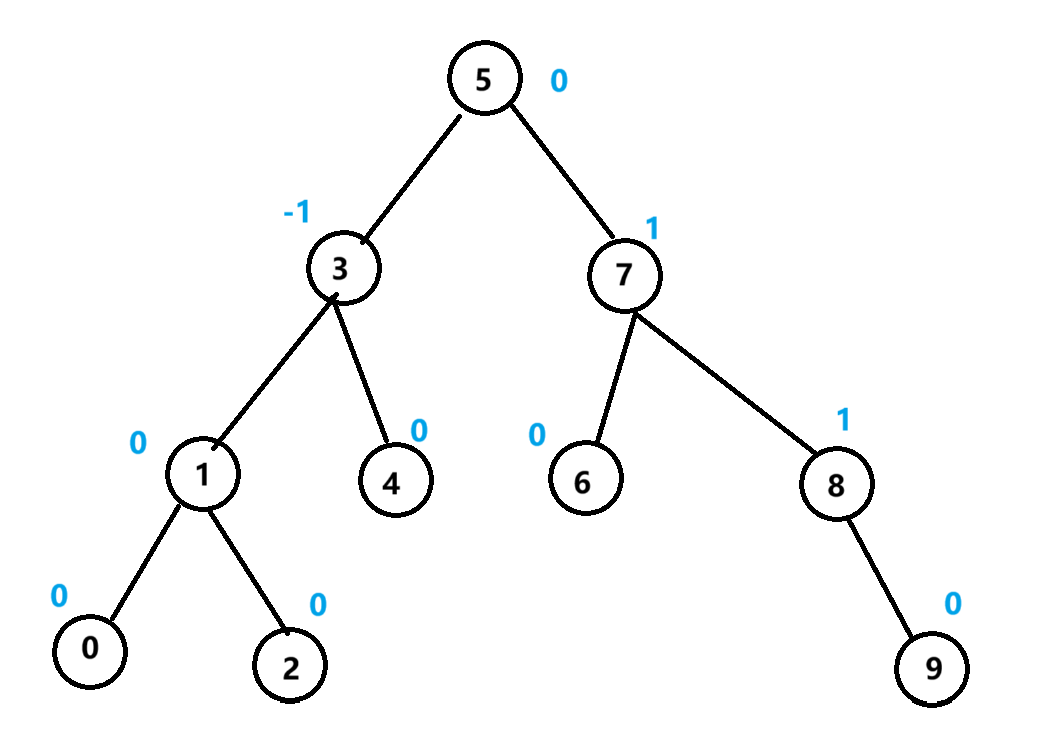
image.png

节点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
template<class K, class V>
struct AVLTreeNode {
	AVLTreeNode<K, V>* _left; // 左子树
	AVLTreeNode<K, V>* _right; // 右子树
	AVLTreeNode<K, V>* _parent; // 父节点

	pair<K, V> _kv; // 键值对

	int _bf; // 平衡因子

	AVLTreeNode(const pair<K, V>& kv)
		:_left(nullptr)
		, _right(nullptr)
		, _kv(kv)
		, _bf(0) {}
};

插入

AVL树与二叉搜索树的区别就是引入了平衡因子，而在插入的时候就需要考虑到

但是插入时就要考虑到破坏平衡因子的条件，我们就需要进行调整，也就是说分两步，按照二叉搜索树的方式插入节点，再对树进行调整

我们用右子树高度减去左子树高度作为该树的平衡因子，因此当左子树插入一个新节点高度加一时，平衡因子减一即可，右子树插入一个新节点高度加一时，平衡因子加一即可

当平衡因子更新之后，就有可能出现不平衡的状态了

  1. 更新后为0，说明更新之前为正负1，插入后调整为0，此时不需要沿父节点向上更新平衡因子
  2. 更新后为正负1，说明更新前为0，插入后调整为正负1，此时需要沿父节点向上更新平衡因子
  3. 更新之后为正负2，此时不平衡，需要进行旋转处理

此时我们就需要对旋转进行分情况讨论了，有四大类情况

右单旋

原本的状态如下

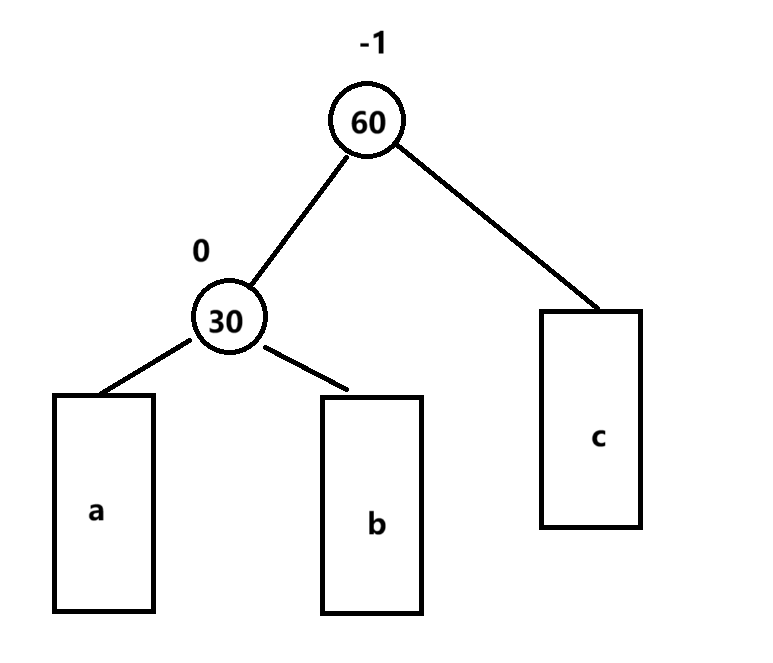
image.png

插入一个新节点

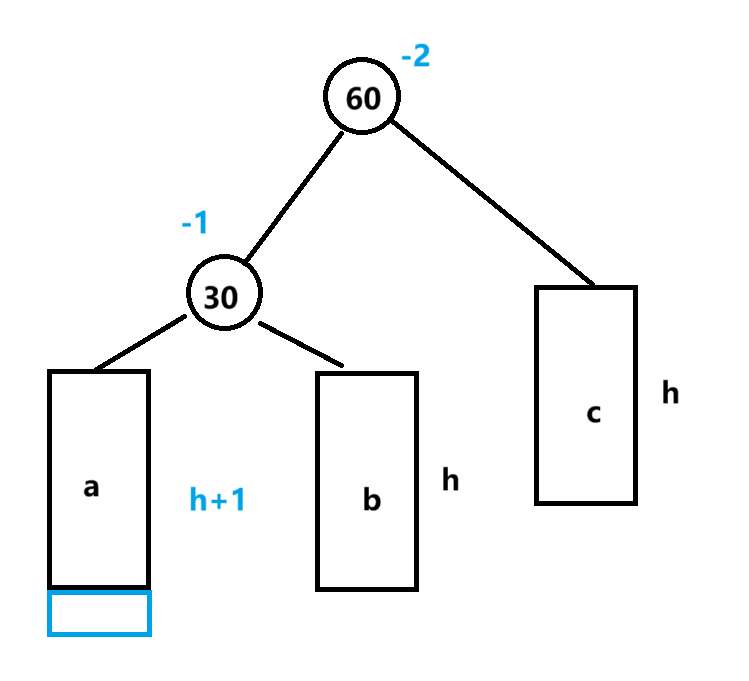
image.png

右单旋

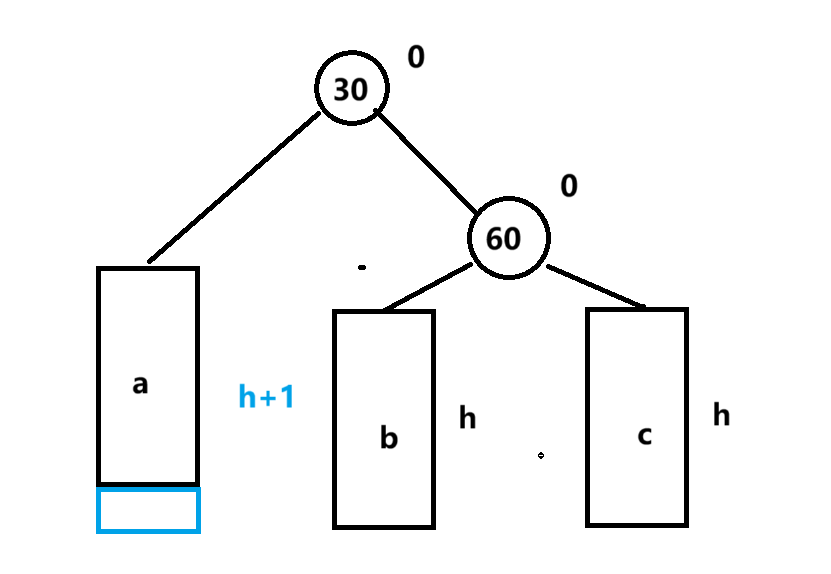
image.png

具体操作是将30的右子树给60的左子树，然后让30做60的父节点，之后更新平衡因子，这里有几点需要考虑，30的右子树有可能不存在，但是不影响结果

60如果是根节点，旋转完成之后需要转换根节点给30，如果是子树，则需要判断他是他父节点的左子树还是右子树，需要更新

左单旋和右单旋情况类似，这里不过多展开

左右双旋

当新插入的节点在较高左子树的右侧时，旋转一次就无法解决问题了，此时就需要先左旋，再右选，如图

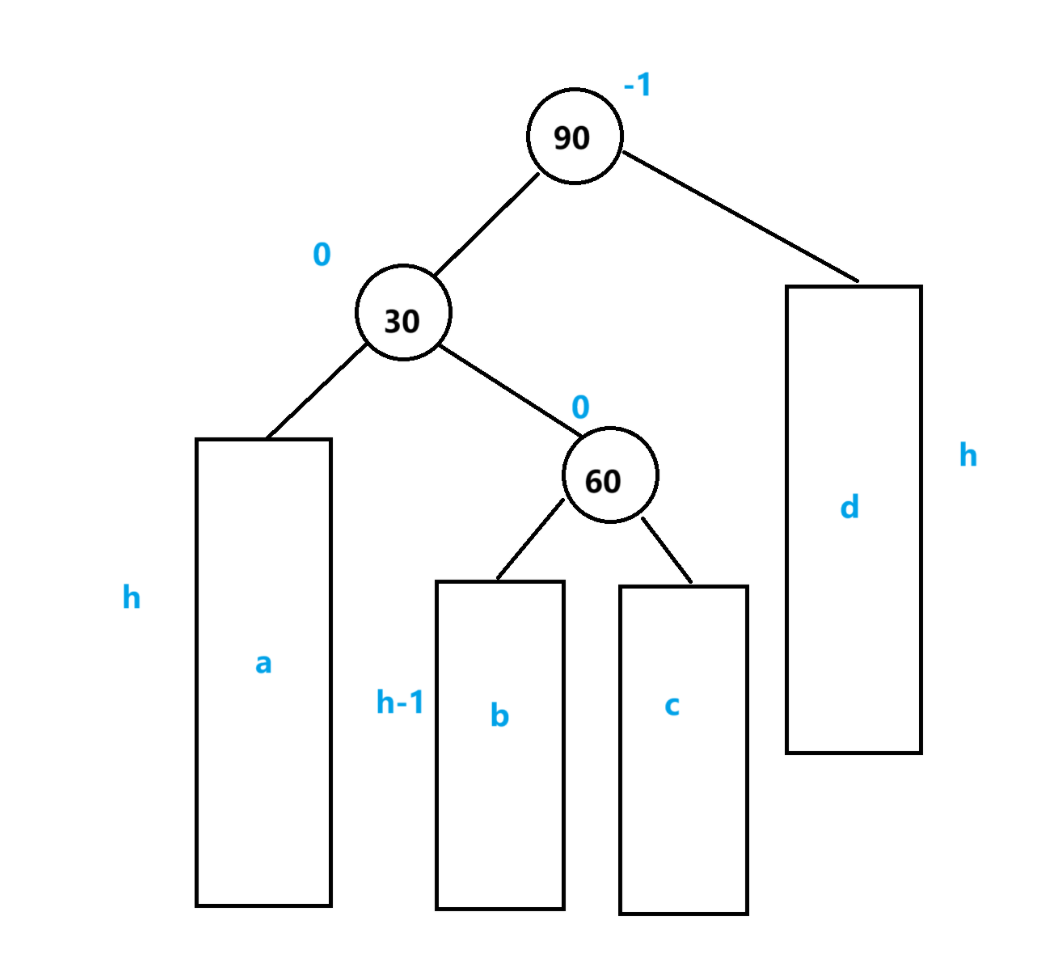
image.png

插入节点

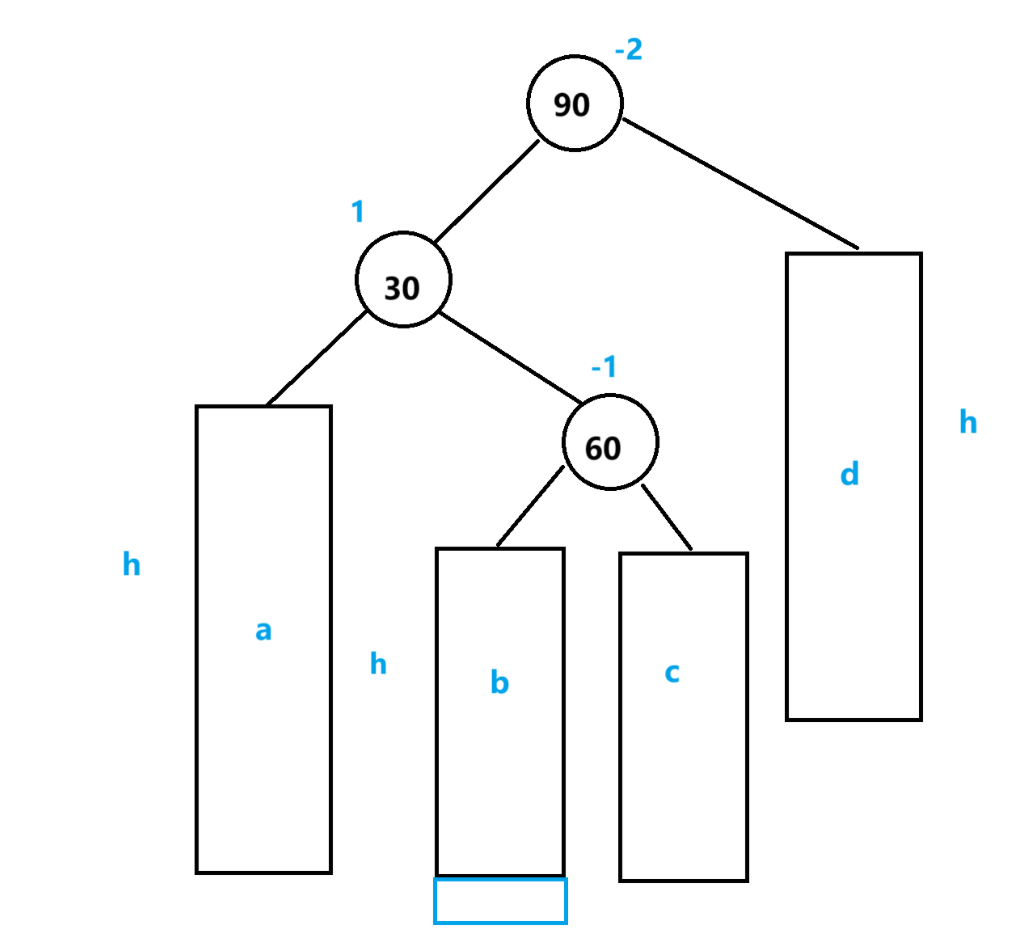
image.png

先以30为中心左单旋

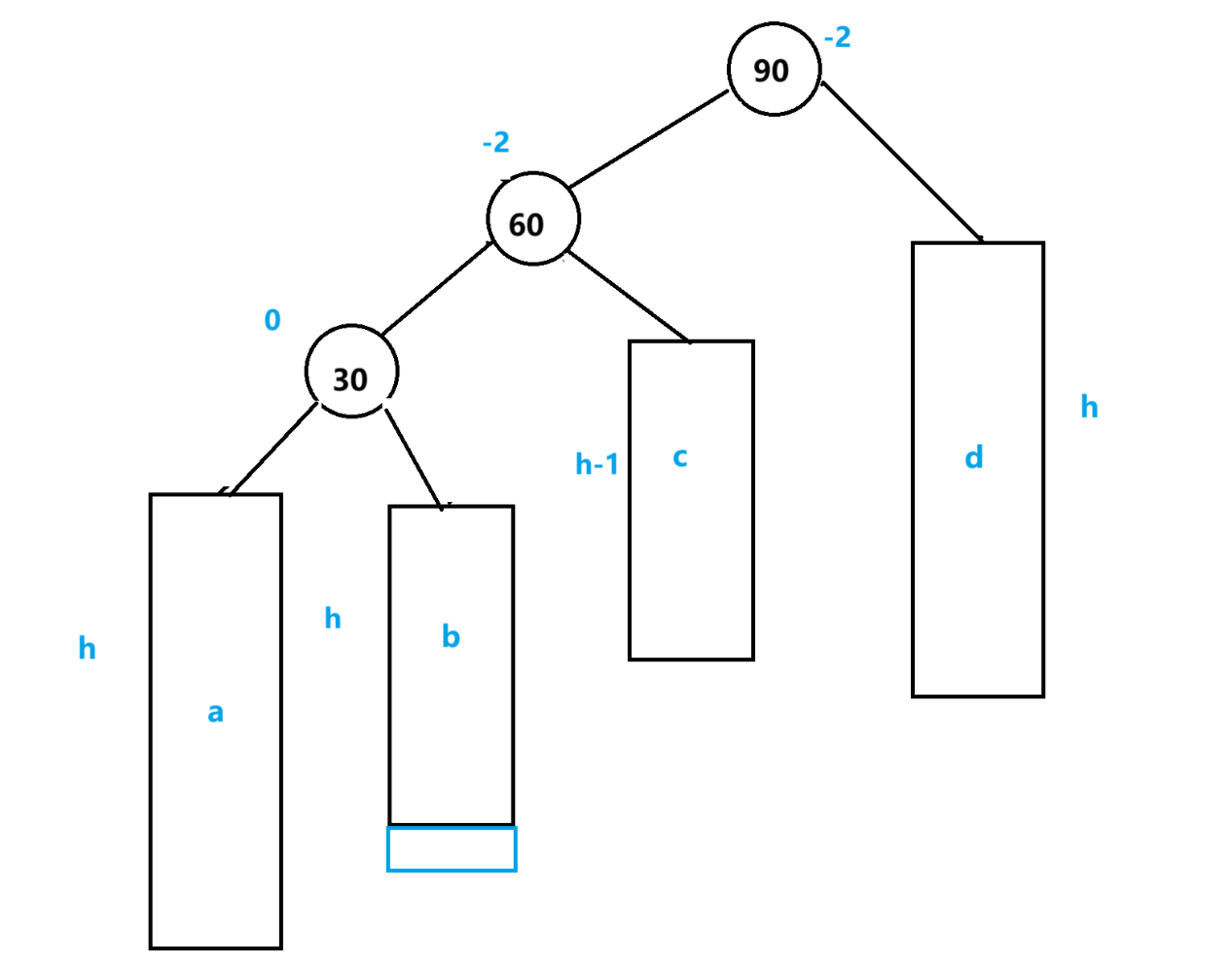
image.png

再以90为中序右单旋

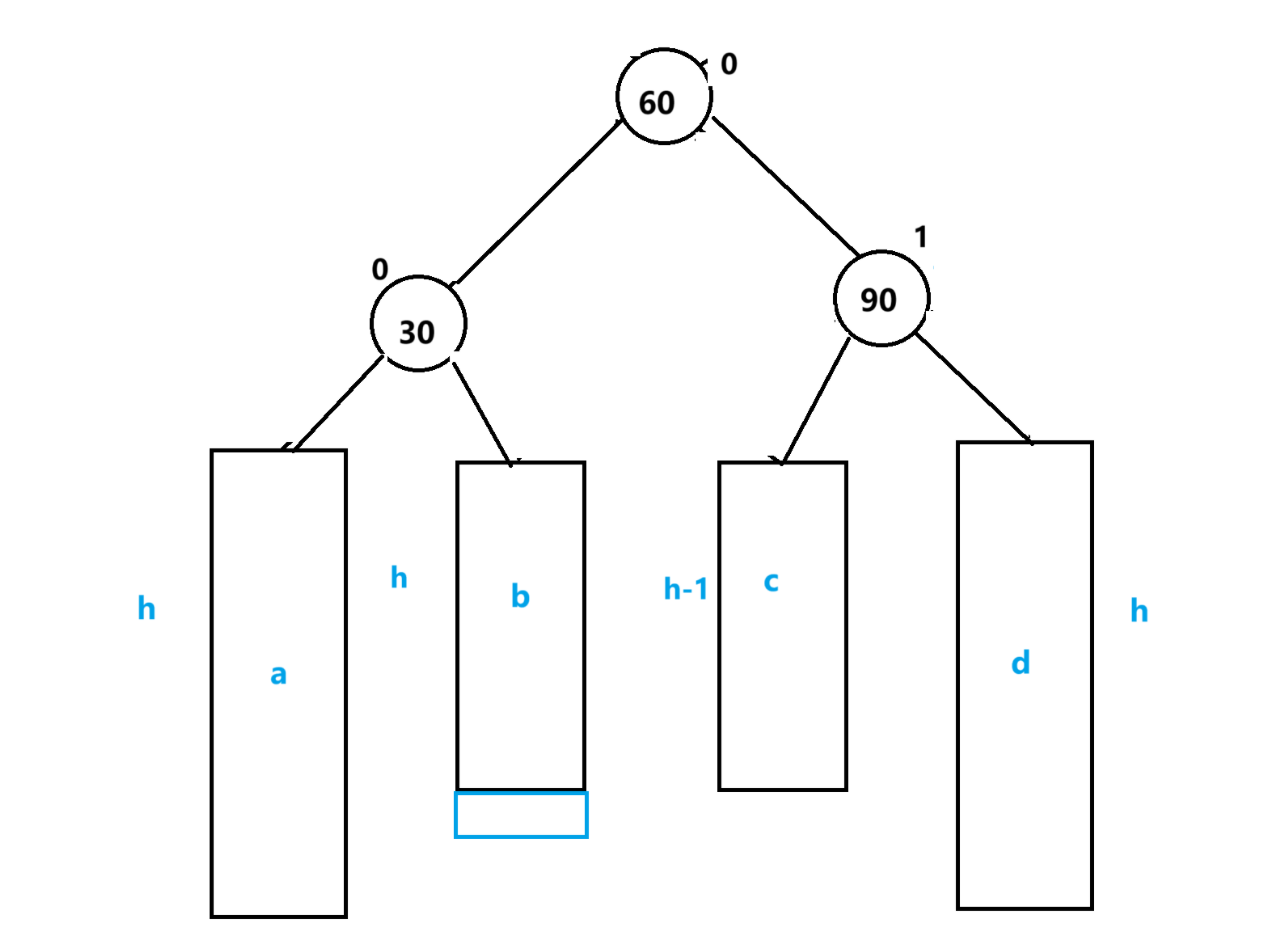
image.png

旋转之后再更新平衡因子即可

同理的，如果是右子树较高的左子树插入，则需要先右旋再左旋

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
template<class K, class V>
class AVLTree {
	typedef AVLTreeNode<K, V> Node;
public:
	bool Insert(const pair<K, V>& kv) {
		if (_root == nullptr) { // 空树直接插入
			_root = new Node(kv);
			return true;
		}

		Node* parent = nullptr;
		Node* cur = _root;

		while (cur) {
			if (cur->_kv.first < kv.first) {
				parent = cur;
				cur = cur->_right;
			} else if (cur->_kv.first > kv.first) {
				parent = cur;
				cur = cur->_left;
			} else {
				return false;
			}
		}

		cur = new Node(kv);
		if (parent->_kv.first < kv.first) {
			parent->_right = cur;
			cur->_parent = parent;
		} else {
			parent->_left = cur;
			cur->_parent = parent;
		}

		while (parent) {
			// 更新平衡因子
			if (cur == parent->_left) {
				parent->_bf--;
			} else {
				parent->_bf++;
			}

			// 开转
			if (parent->_bf == 0) {
				break;
			} else if (parent->_bf == 1 || parent->_bf == -1) {
				cur = parent;
				parent = parent->_parent;
			} else if (parent->_bf == 2 || parent->_bf == -2) {
				if (parent->_bf == 2 && cur->_bf == 1) {
					RotateL(parent);
				} else if (parent->_bf == -2 && cur->_bf == -1) {
					RotateR(parent);
				} else if (parent->_bf == 2 && cur->_bf == -1) {
					RotateRL(parent);
				} else if (parent->_bf == -2 && cur->_bf == 1) {
					RotateLR(parent);
				}
				break;
			} else {
				assert(false);
			}
		}

		void RotateL(Node * parent) {
			Node* subR = parent->_right;
			Node* subRL = subR->_left;

			parent->_right = subRL;
			subR->_left = parent;

			Node* parentParent = parent->_parent;

			parent->_parent = subR;
			if (subRL)
				subRL->_parent = parent;

			if (_root == parent) {
				_root = subR;
				subR->_parent = nullptr;
			} else {
				if (parentParent->_left == parent) {
					parentParent->_left = subR;
				} else {
					parentParent->_right = subR;
				}

				subR->_parent = parentParent;
			}

			parent->_bf = subR->_bf = 0;
		}

		void RotateR(Node * parent) {
			Node* subL = parent->_left;
			Node* subLR = subL->_right;

			parent->_left = subLR;
			if (subLR)
				subLR->_parent = parent;

			Node* parentParent = parent->_parent;

			subL->_right = parent;
			parent->_parent = subL;

			if (_root == parent) {
				_root = subL;
				subL->_parent = nullptr;
			} else {
				if (parentParent->_left == parent) {
					parentParent->_left = subL;
				} else {
					parentParent->_right = subL;
				}

				subL->_parent = parentParent;
			}

			subL->_bf = parent->_bf = 0;
		}

		void RotateRL(Node * parent) {
			Node* subR = parent->_right;
			Node* subRL = subR->_left;
			int bf = subRL->_bf;

			RotateR(parent->_right);
			RotateL(parent);

			if (bf == 0) {
				// subRL自己就是新增
				parent->_bf = subR->_bf = subRL->_bf = 0;
			} else if (bf == -1) {
				// subRL的左子树新增
				parent->_bf = 0;
				subRL->_bf = 0;
				subR->_bf = 1;
			} else if (bf == 1) {
				// subRL的右子树新增
				parent->_bf = -1;
				subRL->_bf = 0;
				subR->_bf = 0;
			} else {
				assert(false);
			}
		}
		return true;
	}
private:
	Node* _root = nullptr;
};

验证AVL树

要验证AVL树有两步

  1. 中序遍历得到有序序列
  2. 验证每个节点的平衡因子的绝对值不大于1，如果没有平衡因子则计算高度差

AVL树的性能

AVL树的查询性能在$\log_2N$，但是如果要更改结构时性能就比较擦汗了，尤其是当旋转次数比较多时，更差的是在删除时，有可能每次都要旋转，因此需要一种查询高效切有序而且数据个数不怎么改变的时候，可以考虑AVL树，不断插入和删除则不合适

Comments