unordered系列关联式容器 之前我们讲到,STL提供了底层为红黑树的一系列关联式容器,可以在相当高的效率下进行查询
但是在树的节点非常多的时候,查询效率也不够理想,因此在C++11中又提供了unordered系列的容器,unordered_map、unordered_set、unordered_multimap、unordered_multiset
这四个容器的使用和原本的map和set基本完全相同,只是没有了排序的功能,也就是没有中序有序的特性,我们可以在文档中看到他的各种使用,这里就不过多赘述了
我们主要想了解他实现的底层原理和封装过程
底层结构 unordered系列的关联式容器他不需要排序的功能,也就意味着他的底层并非红黑树
实际上他的底层使用了哈希结构
需要注意的是,哈希其实是一种思想,是将原先的数据通过某种方法处理过后,对应到另一种数据上的思想;哈希表是哈希的一种应用,是将数据通过处理后,对应到表的某个位置上
哈希的概念 在过往我们学习顺序结构或树状结构进行查找时,是通过一次次的比较来查找,而效率则是取决于查找过程中元素的比较次数
那是否存在一种查找方法是可以不通过任何比较,一次就能从表中得到我们想要的元素呢
我们面向结果来思考的话,可以构造这样一种存储结构,将数据通过某种方法(哈希函数)计算得出一个结果,将这个结果作为表中的位置,这样我们将数据存到对应的位置,如果这样的数据和位置的映射是一一对应的,那么查找和插入就都是常数级的了
当插入元素时,对数据计算,找到位置直接存放
当查询元素时,对数据计算,直接查找该位置的值即可
这种方法叫做哈希方法,哈希函数,或者叫做散列方法,散列函数
构造出来的结构称之为哈希表或者散列表(Hash Table)
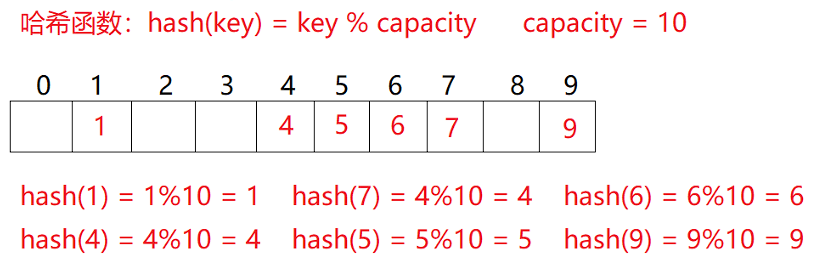
例如
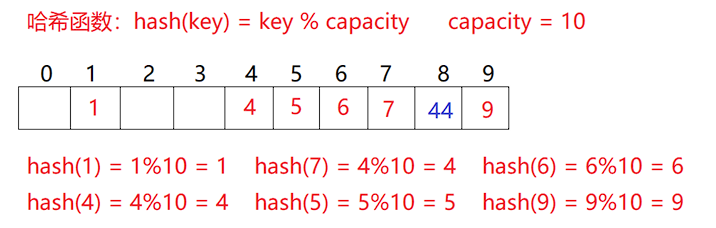
哈希冲突 数据和数据的个数是有无穷多个的,而我们的存储空间和结构却是优先的,这就必定会导致一个问题,就是多个数据通过哈希函数之后对应的位置是相同的,这就产生了哈希冲突或者哈希碰撞
哈希函数 引起哈希冲突的一个可能原因是哈希函数设计不够合理
一般来说哈希函数有如下几个要求
哈希函数的定义域必须包括需要存储的全部关键字,也就是说存储的Key必须能进到哈希函数里计算,当哈希表有m个位置时,值域必须到0-m-1,也就是说必须能存的下,不能越界
哈希函数计算出的地址需要均匀一些
哈希函数不能过于复杂
常见哈希函数
直接定址法
这个方法比较常用,直接将关键字传入某个线性函数得到地址,简单且均匀,适合用于一些查找比较小而且连续的情况
除留余数法
这个方法也比较常用,设散列表中的个数是m,取一个不大于m,接近或者等于的质数作为除数,直接对key进行取模,作为哈希地址
剩下还有就是平方取中法,对一个关键字平方,抽取中间的几位作为哈希地址;折叠法,将关键字分割成几位完全相等的及部分叠加求和,按照哈希表长度取几位作为散列地址;随机数法,直接取随机数作为哈希地址
需要注意的是,哈希函数无论如何设计,只能降低产生哈希冲突的可能性,也就是让数据更为分散的分布,哈希冲突是无法避免的
哈希冲突的解决 闭散列 闭散列也叫做开放定址法,当发生哈希冲突时,将会按照一定规则搜索下一个空位置
搜索下一个空位置的方法也有几个
线性探测法
就是当哈希冲突发生时,顺序找下一个空位置
当删除元素时需要注意,我们不能真的删除对应的元素,而是应当使用标记法删除,因为一旦前面的元素是真删除,变成空了,就会影响后面元素的查找
二次探测
二次探测指的是,当发生冲突时,按照$n^2$来进行探测,找到下一个空位置
开散列 开散列又称连地址法,拉链法,首先对数据进行处理,然后对地址相同的一系列数据归于同一个集合,每一个集合称之为桶,在各个桶中通过单链表连接起来,链表的头节点存于哈希表中
在某些语言,例如Java中,当桶的节点数过多时,会将单链表转化为红黑树,这样效率就能进一步提升,但实际上哈希表本身的效率已经足够高了,一般也用不到红黑树
闭散列模拟实现 这里我们采用线性探测法,二次探测法基本一致
基本框架 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 template <class K >struct HashFunc { size_t operator () (const K& key) return (size_t )key; } }; template <>struct HashFunc <string> { size_t operator () (const string& key) } }; namespace open_xu { enum Status { EMPTY, EXIST, DELETE }; template <class K , class V > struct HashData { pair<K, V> _kv; Status _s; }; template <class K , class V , class Hash = HashFunc<K>> class HashTable { public : private : vector<HashData<K, V>> _tables; size_t _n = 0 ; }; }
最上面的仿函数和之前红黑树实现的类似,红黑树里的仿函数是取出Key对应的T,这里的仿函数是因为不知道Key的类型,例如字符串,不能直接对某个数字取模,因此采用仿函数的方法进行特化
我们使用枚举类型作为表示哈希表中的元素状态
基本函数 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 HashTable () { _tables.resize (10 ); } bool Insert (const pair<K, V>& kv) if (Find (kv.first)) return false ; if (_n * 10 / _tables.size () == 7 ) { size_t newSize = _tables.size () * 2 ; HashTable<K, V, Hash> newHT; newHT._tables.resize (newSize); for (size_t i = 0 ; i < _tables.size (); i++) { if (_tables[i]._s == EXIST) { newHT.Insert (_tables.[i]._kv); } } _tables.swap (newHT, _tables); } Hash hf; size_t hashi = hf (kv.first) % _tables.size (); while (_tables[hashi]._s == EXIST) { hashi++; hashi %= _tables.size ()l; } _tables[hashi]._kv = kv; _tables[hashi]._s = EXIST; ++_n; return true ; } HashData<K, V>* Find (const K& key) { Hash hf; size_t hashi = hf (key) % _tables.size (); while (_tables[hashi]._s != EMPTY) { if (_tables[hashi]._kv.first == key && _tables[hashi]._s == EXIST) { return &_tables[hashi]; } ++hashi; hashi %= _tables.size (); } return nullptr ; } bool Erase (const K& key) HashData<K, V>* ret = Find (key); if (ret) { ret->_s = DELETE; --_n; return true ; } else { return false ; } }
构造函数是默认开了10个位置,注意vector的resize是空间和容量都开到了10
插入的过程中有一步是扩容,这里是为了防止哈希冲突过多,当存储的元素占所有空间的比例大于某一个值时,进行扩容操作
这里的扩容最后将vector的所有内容全部交换了,这样做是完全没有问题的,而且效率也很不错,具体原理在我们模拟实现vector时已经讲过了
最后我们使用仿函数取出值,再取模,得到具体的哈希地址插入即可
删除时使用伪删除
开散列模拟实现 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 namespace hash_bucket { template <class K , class V > struct HashNode { HashNode* _next; pair<K, V> _kv; HashNode (const pair<K, V>& kv) :_kv(kv) ,_next(nullptr ) {} }; template <class K , class V , class Hash = HashFunc<K>> class HashTable { typedef HashNode<K, V> Node; public : HashTable () { _tables.resize (10 ); } ~HashTable () { for (size_t i = 0 ; i < _tables.size (); i++) { Node* cur = _tables[i]; while (cur) { Node* next = cur->_next; delete cur; cur = next; } _tables[i] = nullptr ; } } bool Insert (const pair<K, V>& kv) if (Find (kv.first)) return false ; Hash hf; if (_n == _tables.size ()) { vector<Node*> newTables; newTables.resize (_tables.size () * 2 , nullptr ); for (size_t i = 0 ; i < _tables.size (); i++) { Node* cur = _tables[i]; while (cur) { Node* next = cur->_next; size_t hashi = hf (cur->_kv.first) % newTables.size (); cur->_next = newTables[i]; newTables[hashi] = cur; cur = next; } _tables[i] = nullptr ; } _tables.swap (newTables); } size_t hashi = hf (kv.first) % _tables.size (); Node* newnode = new Node (kv); newnode->_next = _tables[hashi]; _tables[hashi] = newnode; ++_n; return true ; } Node* Find (const K& key) { Hash hf; size_t hashi = hf (key) % _tables.size (); Node* cur = _tables[hashi]; while (cur) { if (cur->_kv.first == key) { return cur; } cur = cur->_next; } return nullptr ; } bool Erase (cosnt K& key) Hash hf; size_t hashi = hf (key) % _tables.size (); Node* prev = nullptr ; Node* cur = _tables[hashi]; while (cur) { if (cur->_kv.first == key) { if (prev == nullptr ) _tables[hashi] = cur->_next; else prev->_next = cur->_next; delete cur; return true ; } prev = cur; cur = cur->_next; } return false ; } private : vector<Node*> _tables; size_t _n = 0 ; }; }
开散列的基本思想是使用一个指针数组分别存放对应的哈希桶,每个指针数组对应一个单链表,表头作为指针数组的元素
我们可以使用内置的forward_list或者list直接构造,但是为了后面我们对哈希表进行封装,这里简单写一个单链表
既然是自己写的单链表,就需要手动写一个析构函数,以防内存泄漏
对于插入函数,也需要检测一下是否需要扩容,这里扩容的操作也可以像闭散列一样,逐一插入再交换,但其实没有必要这样做,单链表本身其实非常灵活,我们可以直接移动节点而非创造和删除节点,扩容之后的插入因为不知道查询的顺序,所以头插和尾插都是可以的,但是尾插需要找到尾部,效率其实没有那么高,因此我们选择头插
查找函数没什么好说的非常简单
删除函数首先需要查找到对应节点,再进行删除,因为这是单链表,不能直接删除,需要连接pre和next节点,所以不能直接复用查找函数,要手动找对应的节点,需要注意的是如果是头删的话要特殊处理一下